Finding Diameter Of A Circle Using Circumference

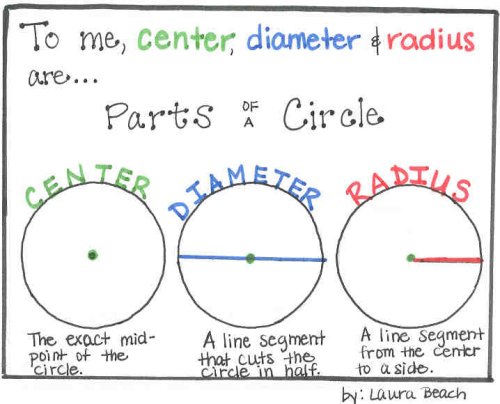
As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle. Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. A circle is a geometric form of which every point on the outside of the circle is the same distance away from the center. The distance around the edge of the circle is called the circumference. The distance from one side of the circle to the other, going through the center of the circle, is the diameter. The constant pi, designated by the Greek letter π, is the ratio of the circumference to the diameter of a circle.

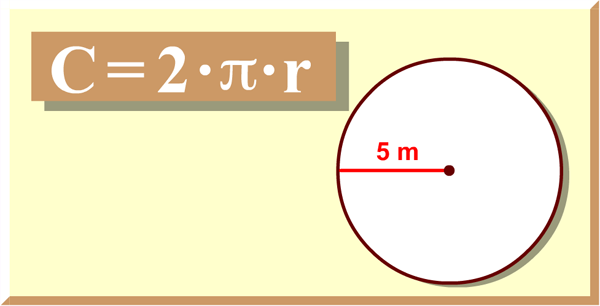
For any circle, if you divide the circumference by the diameter you get pi, an irregular number usually rounded to 3.14. The circumference of a circle of radius $r$ is $2\pi r$. This well known formula is taken up here from the point of view of similarity.

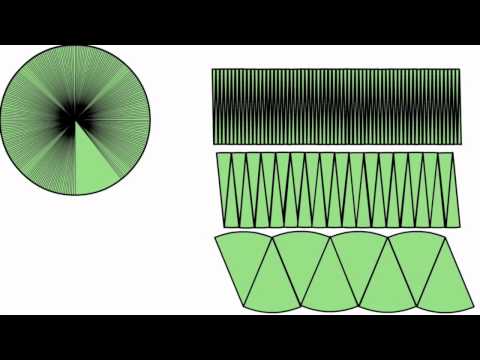
It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle. In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required. Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles. This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle. The circumference of a circle is the measurement around a circle's edge.

It can be compared to finding the perimeter of a shape . If you were to cut a circle and lay the outline flat, the length of the line it created would be its circumference. The circumference can be measured in any unit or system that traditionally measures length - imperial (inches, feet, etc.) or metric (centimeters, meters, etc.). Whichever unit the radius is measured in will also be the unit the circumference is calculated in. To understand how to calculate circumference we must first begin with the definition of circumference.

Circumference of a circle is linear distance around outer border of a circle. To find out the circumference, we need to know its diameter which is the length of its widest part. The diameter should be measured in feet for square footage calculations and if needed, converted to inches , yards , centimetres , millimetres and metres . The learning outcome of this article is that one can calculate the circumference of circular objects and circular paths.

Circle is a particular shape and defined as the set of points in a plane placed at equal distance from a single point called the center of the circle. We use the circle formula to calculate the area, diameter, and circumference of a circle. Radius is half the length of a diameter of the circle. Area of the circle describes the amount of space covered by the circle and the length of the boundary of the circle is known as its circumference. This first argument is an example of MP7, Look For and Make Use of Structure. The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference.

The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles. When the formula for calculating the circumference of a circle is used, the circle's radius is considered. As a result, the radius or diameter value must be known to calculate the circle's perimeter or circumference. The diameter of a circle is twice to that of the radius.

If the diameter or radius of a circle is given, then we can easily find the circumference. We can also find the diameter and radius of a circle if the circumference is given. We round off to 3.14 in order to simplify our calculations. Circumference, diameter and radii are calculated in linear units, such as inches and centimeters.

A circle has many different radii and many different diameters, and each one passes through the center. The diameter is defined as twice the length of the radius of a circle. Does calculating circumference have you running in circles?

Our circumference calculator is an easy way for you to find the circumference of any circular object. As stated before, the perimeter or circumference of a circle is the distance around a circle or any circular shape. The circumference of a circle is the same as the length of a straight line folded or bent to make the circle.

The circumference of a circle is measured in meters, kilometers, yards, inches, etc. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Blame Welsh mathematician William Jones for the trouble pi causes you. In 1706 Jones used the Greek word for circumference, περιϕέρεια, and shortened it to its first letter, π. As for π in circles, we have no one to blame but the marvel that is mathematics.

Pi, or π, is the irrational number that links every circle's circumference to diameter and radius. The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle.

You can also think of the radius as the distance between the center of the circle and its edge. Thus, we can calculate the circumference of a circle if we know the circle's radius . For most calculations that require a decimal answer, estimating π as 3.14 is often sufficient.

For instance, if a circle has a radius of 3 meters, then its circumference C is the following. Is made up of a large number of concentric circular pieces of very thin string. The Greek letter p (pronounced as "pie") is used to describe this number. It stands for the ratio between the circumference of any circle and its diameter, and it's true for all circles. This means that any circle's circumference will be about 3.14 times the length of its diameter.

In all likelihood, the very first wheels were pieces of logs that were mounted on an axle. Gradually, the design of the wheel improved, their design became more and more complex, and for their manufacture it was necessary to use a lot of different tools. First, wheels appeared, consisting of a wooden rim and spokes, and then, in order to reduce wear on their outer surface, they began to upholster it with metal strips. Using this knowledge, you can use the radius or diameter of a circle to find its length. For example, to calculate the circumference of a circle with a radius of 3 cm, you need to multiply the radius by 2 , and multiply the resulting diameter by π. Finally, with the number π we learned that the circumference of a circle with a radius of 3 cm is 18.84 cm.

Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel?

To calculate the diameter of a circle, multiply the radius by 2. If you don't have the radius, divide the circumference of the circle by π to get the diameter. If you don't have the radius or the circumference, divide the area of the circle by π and then find that number's square root to get the radius. Then, you can just multiply the radius by 2 to find the circle's diameter. Using geometrical formulas and equations gets easier with practice. Ask for help from someone who has worked with circles or any other geometrical figures.

You're likely to find that questions of geometry will seem less challenging with a little experience. You can check this relationship of circumference to diameter by putting a piece of string around circular objects of different sizes, such as cans, coins, and plates. Measure the string against a ruler, yard stick, or meter stick to find the circumference. Make a table like the one shown below, showing the diameter and circumference of each object you measure.

This online lesson from onlinemathlearning.com provides a good explanation about how to use either radius or diameter to calculate the circumference of a circle. Acircleis a closed round shape with all the points equidistant from a fixed point known as the centre. The circle's circumference is measured in length units such asmetresandcentimetres.

Similarly, we come across more circular shapes in our everyday life like a dinner plate, Ferris wheel, the dial of a clock, cricket ground, candy, steering wheel, etc. Try the free Mathway calculator and problem solver below to practice various math topics. Try the given examples, or type in your own problem and check your answer with the step-by-step explanations.

Not just this but there are some significant distances on a circle that needs to be calculated before finding the circumference of the circle. Diameter is the distance from one side of the circle to the other, crossing through the center/ middle of the circle. Our circumference calculator will perform all these non-tricky calculations instantly and write the solution in a line with comments. The circumference of objects surrounding us can be measured using a centimeter tape or a rope , the length of which can then be measured separately. In such cases, you can calculate the circumference of a circle if you know the length of its diameter or radius. The distance around a polygon, such as a square or a rectangle, is called the perimeter .

On the other hand, the distance around a circle is referred to as the circumference . Therefore, the circumference of a circle is the linear distance of an edge of the circle. The term circumference is used when measuring physical objects, as well as when considering abstract geometric forms. The circumference of the circular water pit is 18 feet. How can Marcus use this information to determine how long the beam needs to be to go across the center of the pit? Marcus needs to figure out the diameter of the pit.

The distance around a rectangle or a square is as you might remember called the perimeter. The distance around a circle on the other hand is called the circumference . It looks like you calculated the area of a circle using a radius of 2; in this figure, the radius of each circle is 1. To find the area of the figure, imagine the two semi-circles are put together to create one circle. Then calculate the area of the circle and add it to the area of the square. Once again in this example, we're given the radius of the circle.

Although it's not a clean number like our previous example, but we can still simply plug the number directly into the formula like what we did above. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m. The diameter of a circle can be calculated according to the given parameters. If the parameters like radius, circumference, or area are given then we can directly use the following formulas.

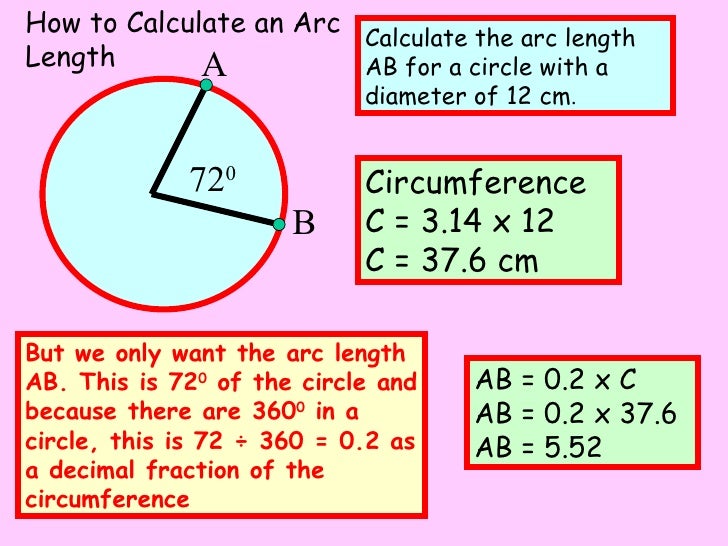
You can think of it as the line that defines the shape. For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference. For example, the length of a 180 degree arc must be half the circumference of the circle, the product of pi and the radius.

The length of any arc is equal to whatever fraction of a full rotation the arc spans multiplied by the circumference of the circle. A 45 degree arc, for example, spans one-eighth of a full rotation, and is therefore equal to one-eighth the circumference of that circle. The length of an arc of n degrees equals (n/360) times the circumference. This constant ratio of circumference to diameter is represented by the Greek letter π and is approximately equal to 3.14 or \(\frac\).

This tool will calculate the diameter of a circle from the circumference, and will convert different measurement units for circumference and diameter. The circumference's ratio to its diameter is fixed in any circle drawn with any radius. This ratio is represented using the Greek letter . If we take any circular objects around us and find the ratio of the circumference to its diameter, it is always a fixed constant (\pi ). Take a whole loop and when you reach that point, stop your loop.

Basically, the perimeter of a circle is the length around a circle. Mathematicians gave it a special name of a circle's perimeter, they call it circumference. Some people also call it the boundary of a circle. In nutshell, the circumference is the length around a circle, that is to say, it is the perimeter of the circle.

And as Math Open Reference states, the formula takes the circumference of the entire circle (2πr). It reduces it by the ratio of the degree measure of the arc angle to the degree measure of the entire circle . Worksheetto calculate circumference of circle when given diameter or radius.

The ratio of the length of a circle to its diameter is the same for all circles. This ratio is a number that is mathematical constant, which is denoted by the Greek letter π. From this we can conclude that the ratio of the circumference of a circle to its diameter is a constant value for each individual circle and for all circles as a whole.